负载牵引轮廓使我们能够考虑器件的非线性响应,并且可以用来设计 PA,就像我们在设计小信号放大器时使用恒定增益或噪声系数轮廓一样。它们还可以考虑放大器的封装寄生效应,尽管这主要超出了本文的范围。
射频设计软件工具通常包括专门用于执行负载牵引测量的仿真工具。这些工具在史密斯圆图上应用了许多不同的负载阻抗,并对结果进行插值,以构建恒定输出功率的轮廓。
如果我们有器件输出和封装寄生效应的等效电路模型,我们也可以相对容易地估算恒定功率的等值线。在本文的其余部分,我们将看到如何(尽管我们暂时将寄生效应排除在我们的分析之外)。

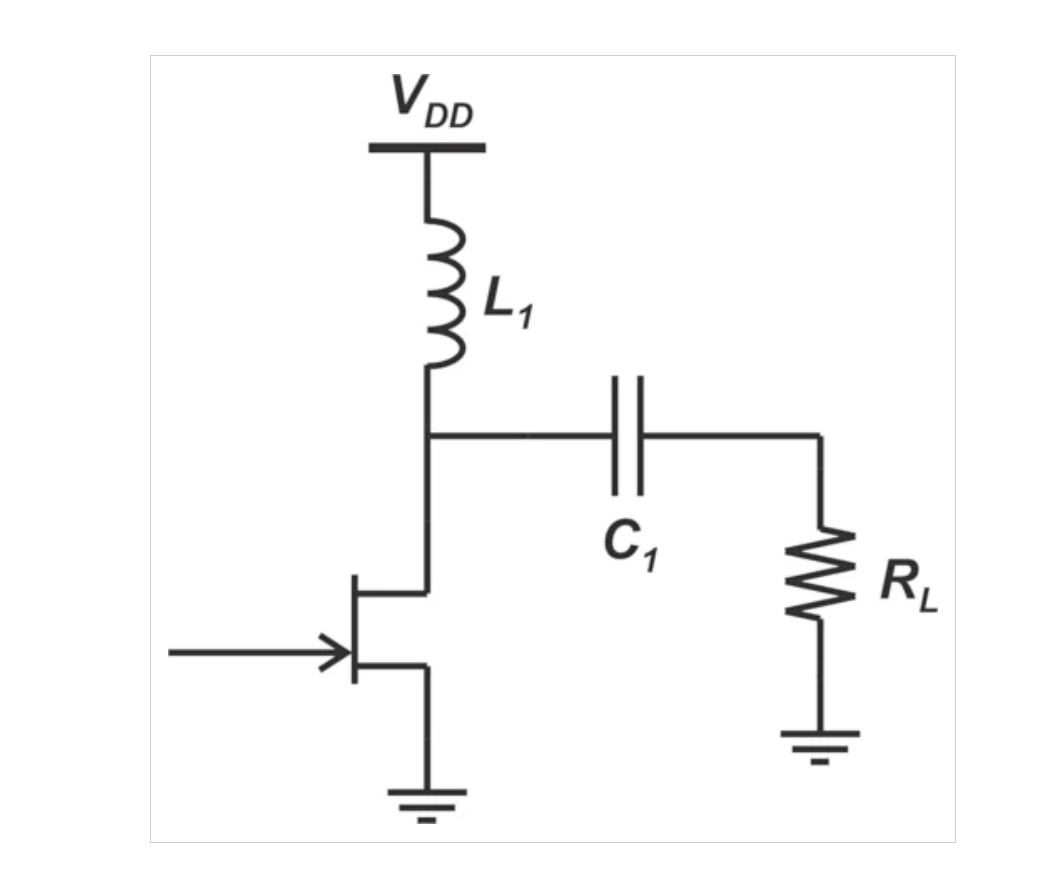
示例功率放大器的特性曲线和最佳负载线。示例PA的特性曲线(蓝色)和最佳负载线(绿色)。图片由Steve Arar提供
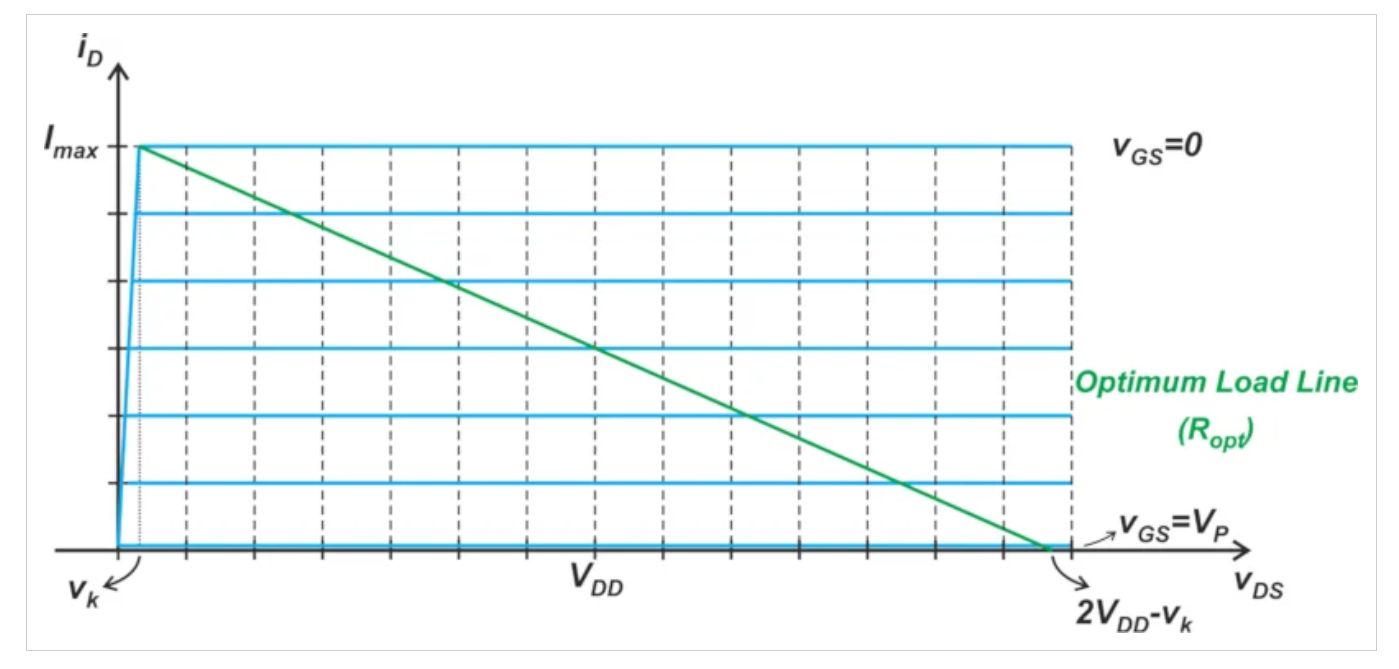
首先,让我们找到我们的示例放大器的最佳负载和功率。为了实现最大输出功率,我们选择适当的负载电阻来偏置负载线中间的晶体管。在vk远小于VDD的情况下,最佳偏置点为VDSQ=3.5V和IDQ=0.5A。我们使用偏置点和图3中的信息来找到最佳负载电阻:
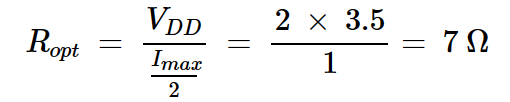
该功率放大器的最佳输出功率为Popt = 0.875 W,实现最佳负载电阻为Ropt = 7 Ω。
三条不同负荷线的图形,其中一条高于最佳负荷线.示例A类放大器的负载线。Ropt为绿色,RL Ropt为紫色,RL Ropt为橙色。图片由Steve Arar提供
电路仍然具有最大电压摆动。但是,与最佳负载相比,它的电流摆动较小。由于电压摆动等于最佳负载的电压摆动,我们可以根据电压写出输出功率,以便更容易与Popt进行比较:
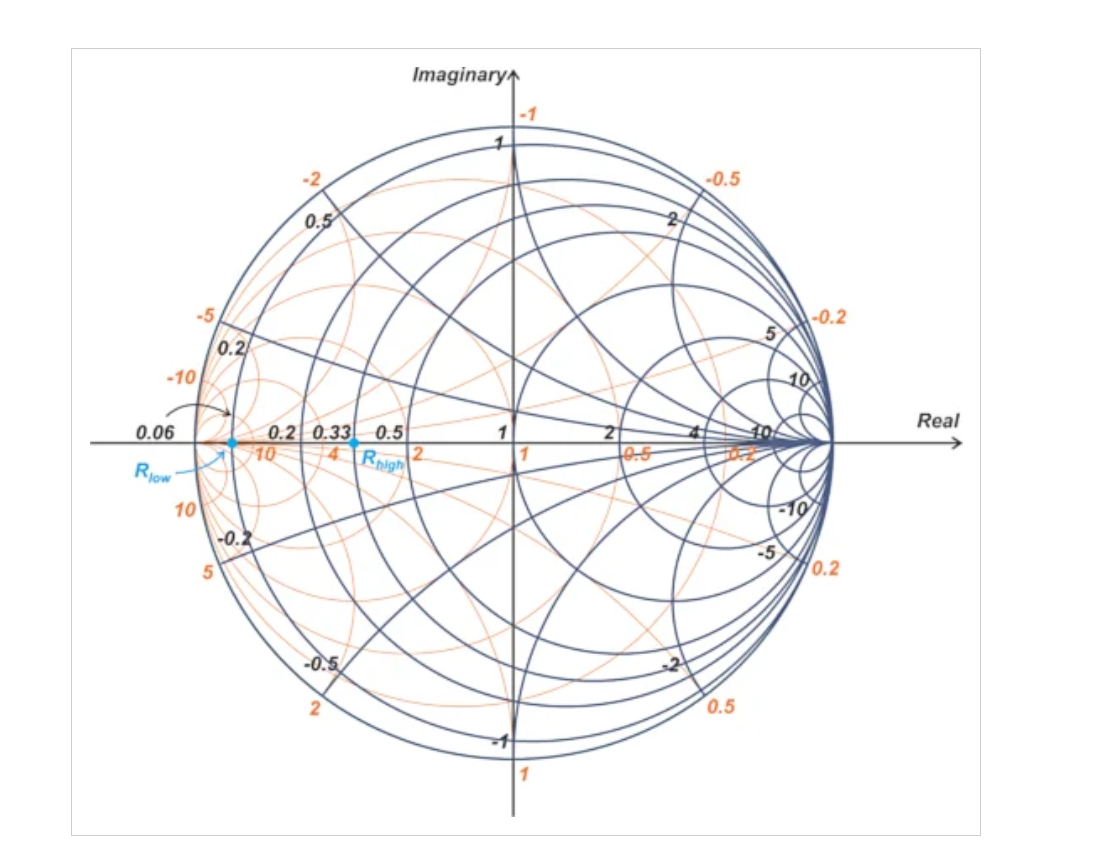
为了在史密斯圆图(图6)上表示我们的结果,我们将Rlow和Rhigh归一化为50Ω。这产生了归一化值0.06和0.33(3/50和16.33/50),分别。
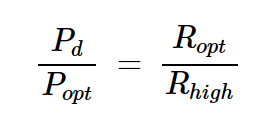
总结一下我们迄今为止学到的内容:如果最大输出功率为Popt,我们可以应用方程5和8来找到两个不同的电阻负载(Rlow和Rhigh),产生输出功率Pd。但是,如果我们使用复杂的终端而不是纯电阻负载,会发生什么?让我们来找出答案。
传输到负载的平均功率仍然由方程2给出。然而,增加的电抗会影响负载两端的电压。当RLRopt时,最大峰峰电流摆幅为Imax,因此ZL的复阻抗的最大峰峰电压摆幅为:
代入Ropt = 7 Ω和Rlow = 3 Ω,我们观察到Xlow必须小于或等于6.32 Ω,对应于归一化值0.13。图7中的蓝色曲线的阻抗,Xlow ≤ 0.13。
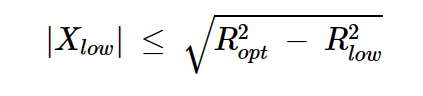
图7.史密斯圆图显示了将电抗添加到Rlow后最终输出功率轮廓的部分。图片由Steve Arar提供
现在我们已经为Rlow添加了一个反应性组件,让我们考虑对Rhigh做同样的事情。当RLRopt时,负载上的最大峰间电压摆动是恒定的(约2VDD)。因此,我们可以将负载描述为导纳而不是阻抗,从而简化我们的方程。假设负载导纳为:
在上面的图中,这两个圆分别表示为r = 0.06和g = 3.1。轮廓从电阻性负载延伸到r = 0.06和g = 3.1圆相交的点。这不是巧合,对于任意期望的输出功率值都会发生这种情况。
这一观察大大简化了寻找恒定功率轮廓的过程——我们只需要使用方程 5 和 8 找到轮廓的电阻点(Rlow 和 Rhigh)。然后,我们找到穿过 Rlow 的恒定电阻圆和穿过 Rhigh 的恒定电导圆的交点。
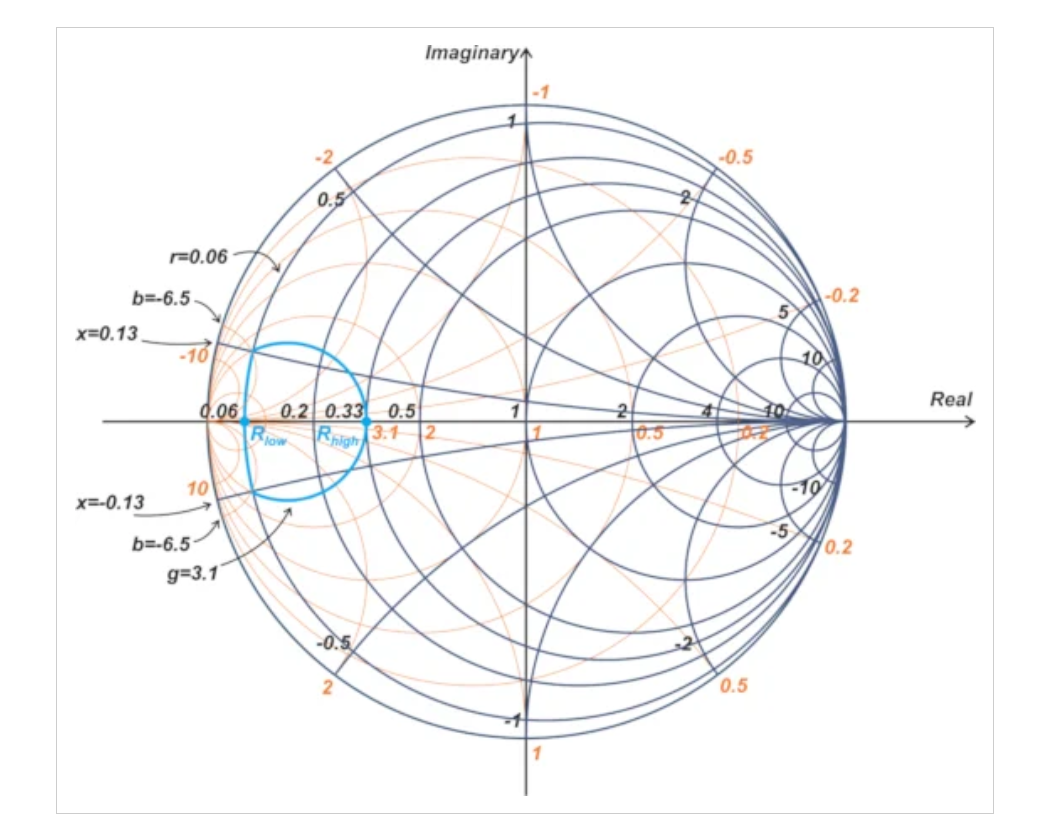
图9.示例PA的三个恒定输出功率轮廓,标记为绿色、蓝色和紫色。图片由Steve Arar提供
_微密圈网页版">发布时间: 2025-07-05 作者:产品中心
详细介绍
功率放大器(PA)的输出功率和效率在很大程度上取决于其负载终端。了解如何通过分析负载线并估计恒定输出功率的负载牵引轮廓来表征PA的性能。
有源射频电路的源端和负载端会影响设备性能的重要方面。这就是为什么当我们设计射频放大器时,我们需要表征有源器件在不同终端阻抗下的性能。在功率放大器(PA)设计中,我们需要特别注意负载阻抗。PA的负载端对它的输出功率和效率有很大的影响,换句话说,对它的主要性能指标有很大的影响。
对于小信号放大器来说,用S参数来描述器件通常就足够了,但PA表现出高度的非线性。因此,经典的小信号S参数不能为我们提供对其性能的充分描述。对于PA,我们需要在使用大信号激励时,针对不同负载阻抗值来表征器件性能。这可以通过一种概念上简单但非常有效的方法来实现,即负载牵引测量。
负载牵引测量是一种通用技术,其中对受试设备(DUT)呈现的负载阻抗系统地变化。然后记录每个负载值的性能,并使用该数据获得感兴趣的性能指标的恒定性能轮廓。
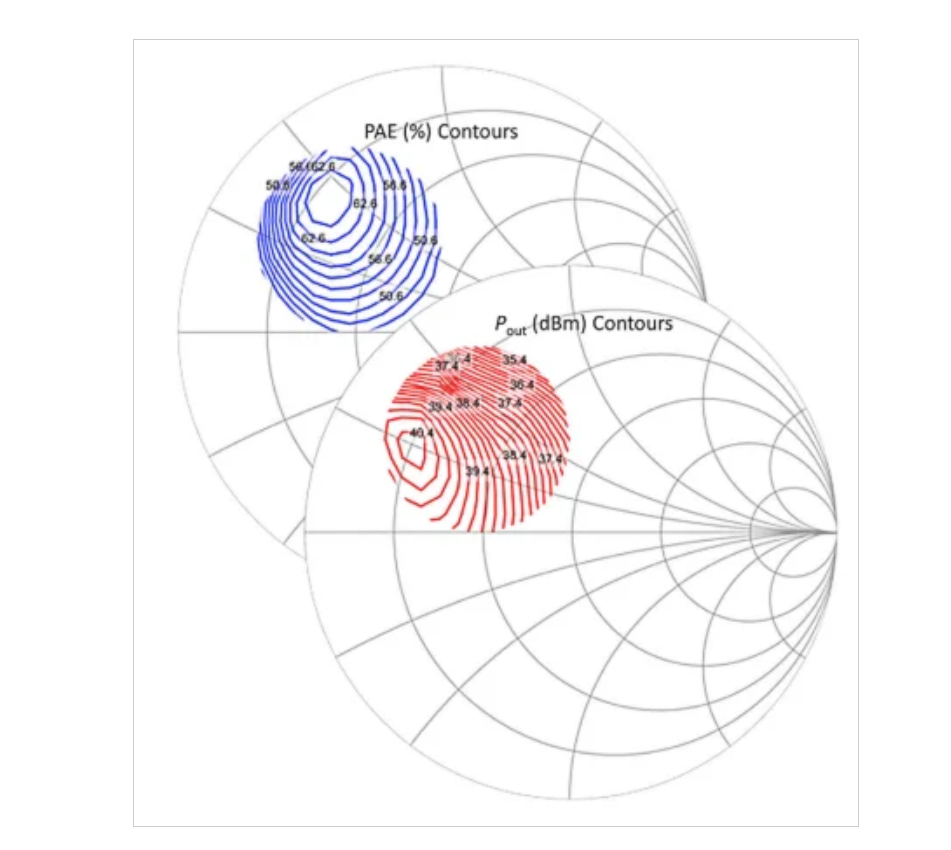
使用负载牵引技术,我们可以在阻抗平面上绘制恒定输出功率和效率的等值线。最好使用史密斯圆图来完成。图1显示了一个典型PA的输出功率(Pout)和功率附加效率(PAE)的一些负载牵引等值线。
负载牵引轮廓使我们能够考虑器件的非线性响应,并且可以用来设计 PA,就像我们在设计小信号放大器时使用恒定增益或噪声系数轮廓一样。它们还可以考虑放大器的封装寄生效应,尽管这主要超出了本文的范围。
射频设计软件工具通常包括专门用于执行负载牵引测量的仿真工具。这些工具在史密斯圆图上应用了许多不同的负载阻抗,并对结果进行插值,以构建恒定输出功率的轮廓。
如果我们有器件输出和封装寄生效应的等效电路模型,我们也可以相对容易地估算恒定功率的等值线。在本文的其余部分,我们将看到如何(尽管我们暂时将寄生效应排除在我们的分析之外)。

示例功率放大器的特性曲线和最佳负载线。示例PA的特性曲线(蓝色)和最佳负载线(绿色)。图片由Steve Arar提供
首先,让我们找到我们的示例放大器的最佳负载和功率。为了实现最大输出功率,我们选择适当的负载电阻来偏置负载线中间的晶体管。在vk远小于VDD的情况下,最佳偏置点为VDSQ=3.5V和IDQ=0.5A。我们使用偏置点和图3中的信息来找到最佳负载电阻:

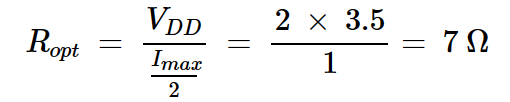
该功率放大器的最佳输出功率为Popt = 0.875 W,实现最佳负载电阻为Ropt = 7 Ω。
三条不同负荷线的图形,其中一条高于最佳负荷线.示例A类放大器的负载线。Ropt为绿色,RL Ropt为紫色,RL Ropt为橙色。图片由Steve Arar提供
电路仍然具有最大电压摆动。但是,与最佳负载相比,它的电流摆动较小。由于电压摆动等于最佳负载的电压摆动,我们可以根据电压写出输出功率,以便更容易与Popt进行比较:
为了在史密斯圆图(图6)上表示我们的结果,我们将Rlow和Rhigh归一化为50Ω。这产生了归一化值0.06和0.33(3/50和16.33/50),分别。
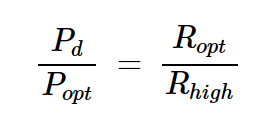
总结一下我们迄今为止学到的内容:如果最大输出功率为Popt,我们可以应用方程5和8来找到两个不同的电阻负载(Rlow和Rhigh),产生输出功率Pd。但是,如果我们使用复杂的终端而不是纯电阻负载,会发生什么?让我们来找出答案。

传输到负载的平均功率仍然由方程2给出。然而,增加的电抗会影响负载两端的电压。当RLRopt时,最大峰峰电流摆幅为Imax,因此ZL的复阻抗的最大峰峰电压摆幅为:
代入Ropt = 7 Ω和Rlow = 3 Ω,我们观察到Xlow必须小于或等于6.32 Ω,对应于归一化值0.13。图7中的蓝色曲线的阻抗,Xlow ≤ 0.13。
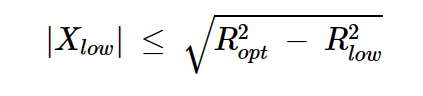
图7.史密斯圆图显示了将电抗添加到Rlow后最终输出功率轮廓的部分。图片由Steve Arar提供
现在我们已经为Rlow添加了一个反应性组件,让我们考虑对Rhigh做同样的事情。当RLRopt时,负载上的最大峰间电压摆动是恒定的(约2VDD)。因此,我们可以将负载描述为导纳而不是阻抗,从而简化我们的方程。假设负载导纳为:
在上面的图中,这两个圆分别表示为r = 0.06和g = 3.1。轮廓从电阻性负载延伸到r = 0.06和g = 3.1圆相交的点。这不是巧合,对于任意期望的输出功率值都会发生这种情况。
这一观察大大简化了寻找恒定功率轮廓的过程——我们只需要使用方程 5 和 8 找到轮廓的电阻点(Rlow 和 Rhigh)。然后,我们找到穿过 Rlow 的恒定电阻圆和穿过 Rhigh 的恒定电导圆的交点。

图9.示例PA的三个恒定输出功率轮廓,标记为绿色、蓝色和紫色。图片由Steve Arar提供
产品咨询